多路PWM脉宽调制电路-PWM转DAC
前言
一些低主频芯片需要高分辨率DAC输出音频信号
单路PWM输出的基本结构如下
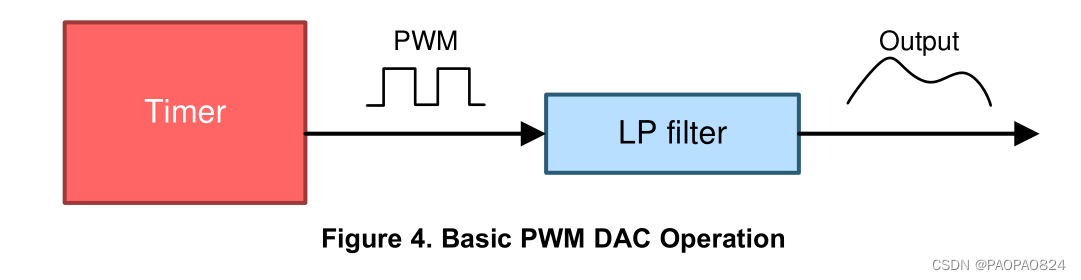
计算一个定时器产生一个PWM时,PWM频率与主频关系如下图
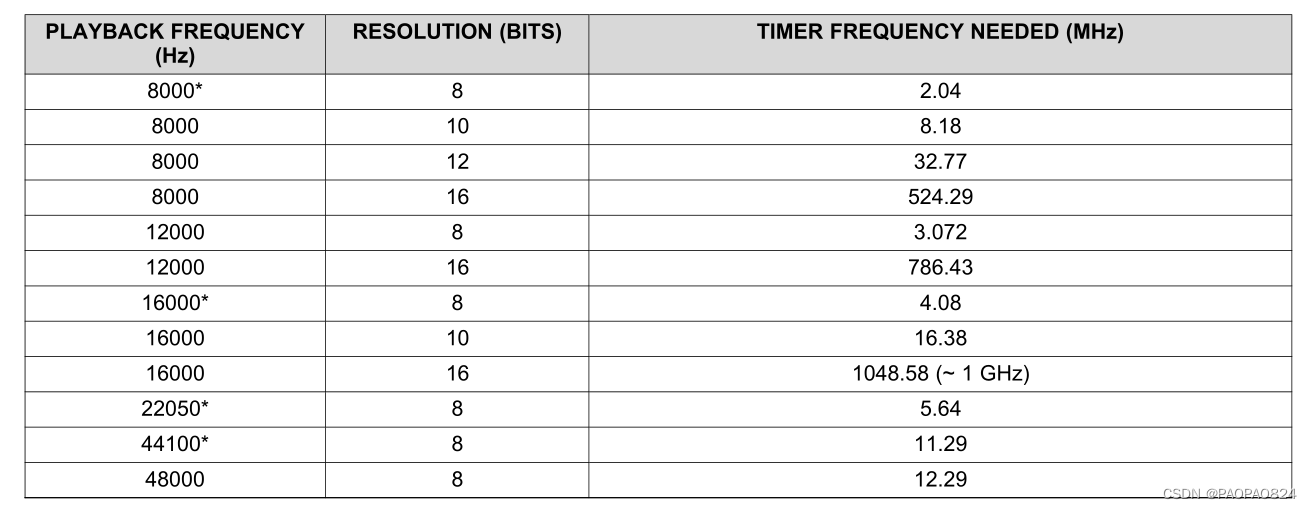
一般MCU输出的音频文件频率是8K/12K/16K,
如果输出8bit分辨率的PWM 主频需要2/3/4MHz
如果输出16bit分辨率的PWM 主频需要524/786/1048MHz,此时一般MCU已经实现不了了。
此时想要高分辨率输出单PWM已经实现不了。
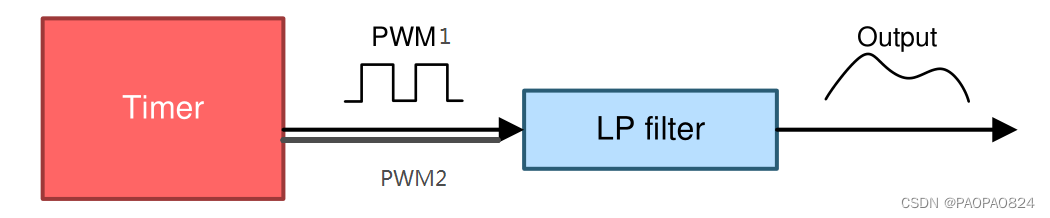
但是用双PWM可以实现输出16bit分辨率,这里使用分割法,把信号分为低位和高位两个PWM分别输出后通过硬件叠加合成,这样可以实现16bit分辨率的输出。
电路结构如下:在PWM1下多一路PWM2,合成后经过滤波器
分析过程
- PWM波形如下图
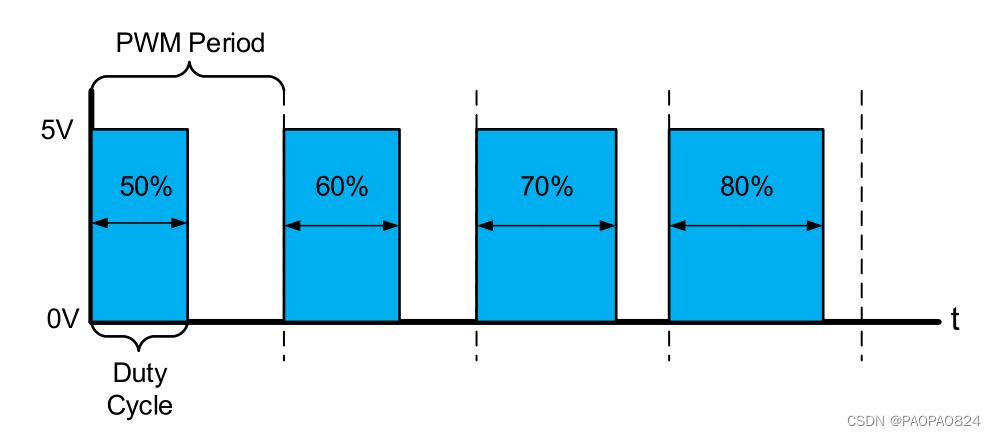
Vout=A x DutyCycle,A 是高电平电压
PWM傅里叶变换后:
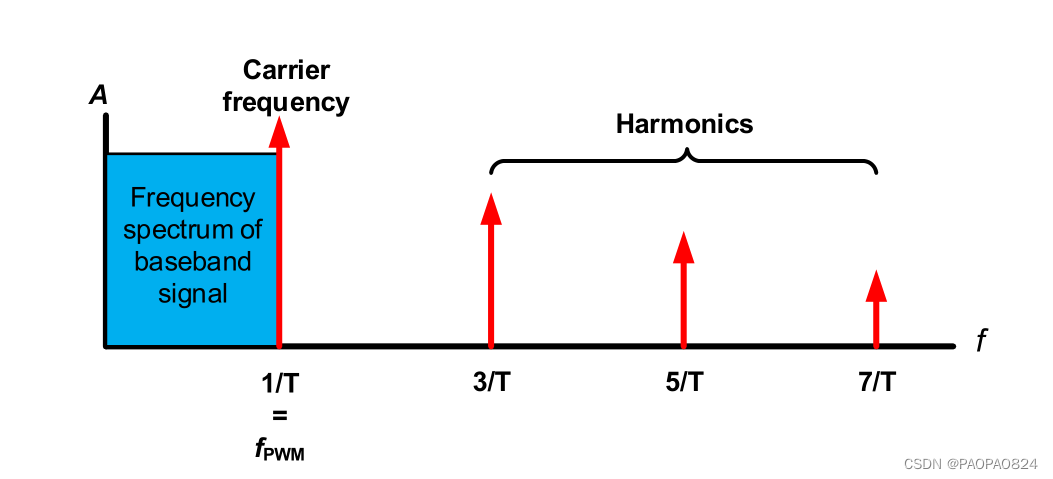
图形可以看出,包含有直流分量与谐波分量(是PWM频率的奇倍数)。
所以如果想得到想要的带宽需要加滤波器,我们知道听觉带宽是20-20KHz(人耳可分辨范围),经过数字采样后得到的数字信号载波频率至少是有效信号的的两倍即40K,信号频率依然是20-20KHz
高通滤波器不合适,带通滤波器需要满足(2N+1)/T<fcmin<20,20k<fcmax<(2N+3)/T显然也无解。
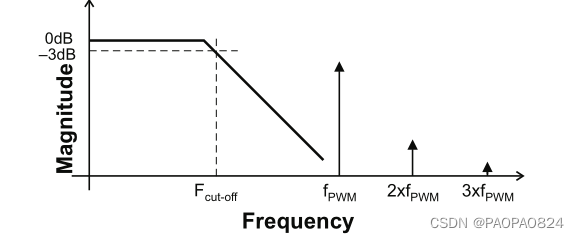
因此用低通滤波器最合适。如下图fc是低通滤波器的截止频率也是我们需要的最高频率,fPWM是pwm的谐波不是我们想要的。
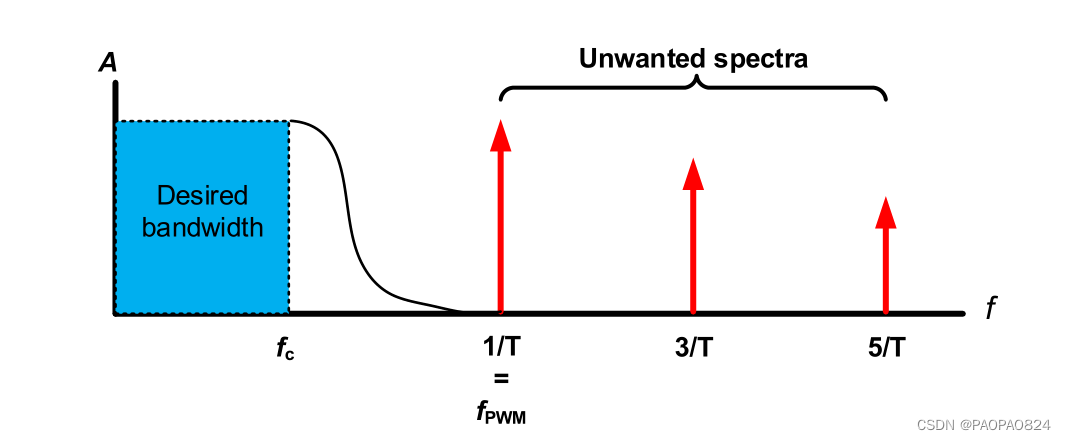
PWM经过低通滤波器后的波形
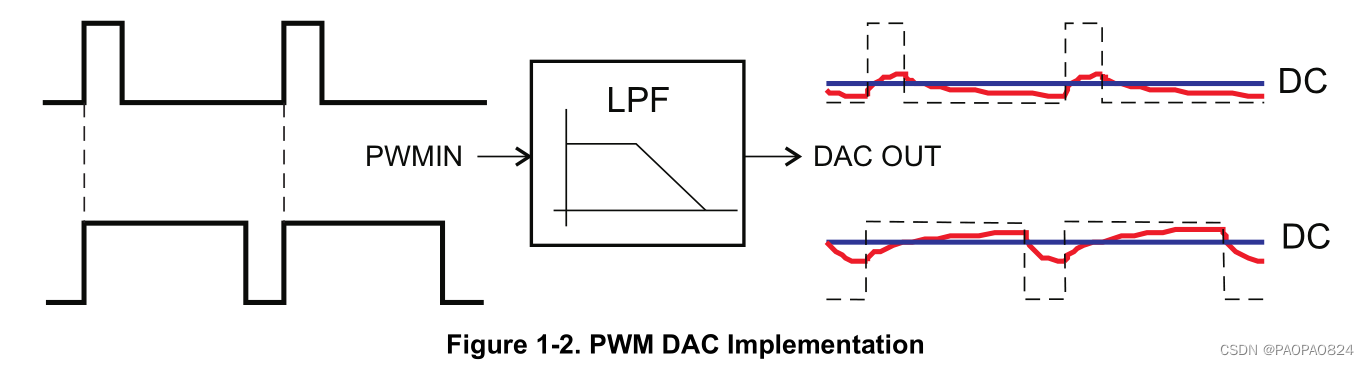
8bit分辨率PWM与等效DAC输出分辨率对应关系如下
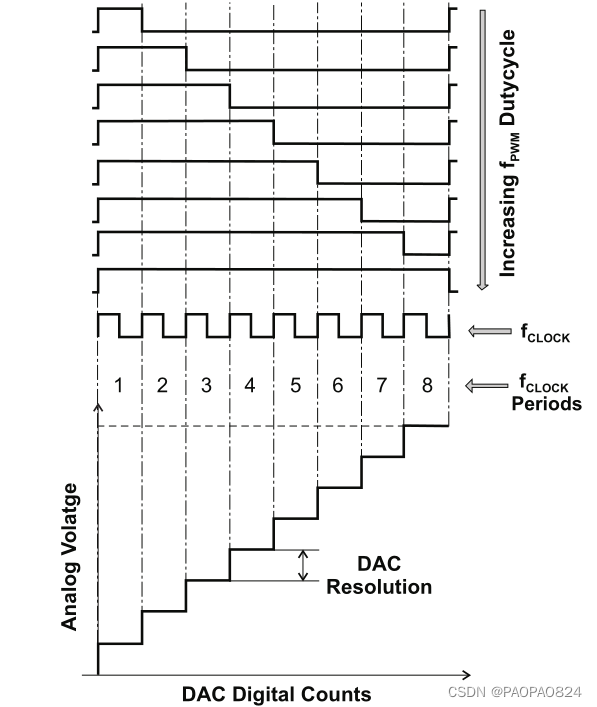
PWM等效DAC的分辨率与输出频率关系:频率越高等效分辨率越低。
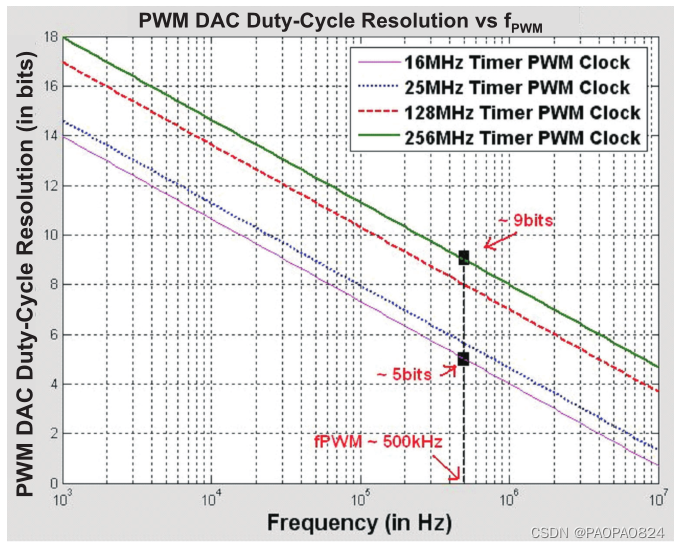
- 分析PWM-DAC等效分辨率与低通滤波器关系以及相关参数取值
- 2.1 我们知道低通滤波器的效果如下:
- 2.2 计算等效分辨率的精度
假如是有效位8bit的分辨率,此时输出可分辨的最小阶梯 Vdac=V/256,V为电源电压
此时PWM载波+信号经过LPF滤波器后,PWM的高次谐波被抑制了但依然有幅度,如下
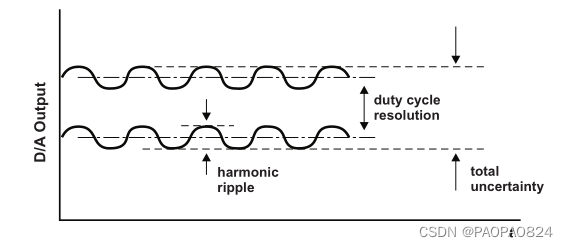
我们要求此时谐波的振幅最少需要小于Vdac/2(分辨率的一半),才可以方便出最小阶梯 Vdac。
因此对LPF有要求,除了截止频率,还需要跟高的阻带衰减率。考虑成本和噪声一半选用RC低通滤波器,下面是一阶和二阶的低通滤波器计算

RC滤波越多阻带衰减率越高。
下面是PWM载波+信号的等效分辨率计算公式

其中:
分母中左边项是PWM等效DAC的分辨率(输入信号)的影响公式如下((VPWMn-VPWMn-1)/Vp-p)

分母中右边项是PWM分辨率的的影响公式如下(例如8bit的PWM则该值为256)

等效分辨率的公式可以分析出:

LPF为一阶RC滤波器10k的带宽时,PWM的频率,主频,以及等效分辨率的关系如下图:
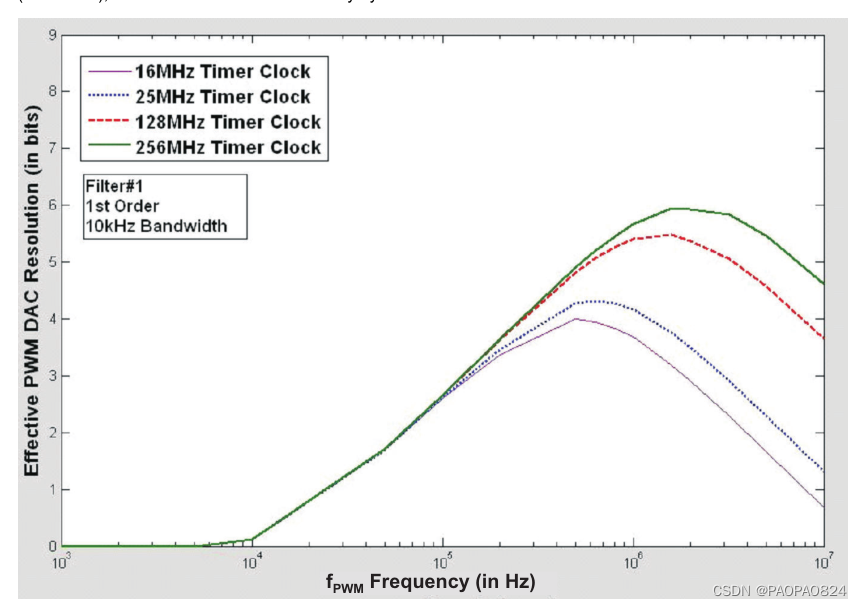
其中随着滤波器带宽增大,整个波形往右平移,即等效分辨率取最大值时pwm的频率也增大,但是等效分辨率不会增大。
LPF为二阶RC滤波器10k的带宽时,PWM的频率,主频,以及等效分辨率的关系如下图:

此时滤波器带宽没变,但是最高等效分辨率增大,以及此时对应的PWM频率减小,这是我们需要的。即pwm频率低同时PWM-DAC等效分辨率高。
因此低通滤波器我们一般选用二阶或者三阶RC低通滤波器。
此时LPF的截止频率fc需要小于fpwm,但是要大于信号的频率(否则有失真),为了获得更好的分辨率截止频率fc尽量靠近信号的最大频率,这样尽可能的滤掉了pwm的高次谐波。
而PWM的频率至少是信号带宽的两倍。
因此一般选择是:
假如信号带宽是16K时,PWM频率选择4倍信号带宽即64K,此时设计LPF的截止频率为20K或者18K时比较好。
多路PWM分析
- 由上面分析知道,一般mcu无法实现一路PWM输出DAC等效分辨率为16bit,此时需要两路或者三路才能达到DAC等效分辨率为16bit。
实现过程是把16bit信号分成两部分,高8位和低8位,分别单独一个PWM输出,输出后通过硬件分压再叠加合成一个信号,后面再过LPF滤波器。
电路结构如下图,其中R2/R1=258

因为PWM1和PWM2的频率一样,PWM1经过R1,C,PWM2经过R2,C,而且R1<R2;因此滤波器的截止频率取R1,C
- 多PWM的要点
上图中通过硬件合成分离的高低位信号,合成后的信号再经过LPF,分析过程如同上面单路PWM。
我们知道这是通过硬件RC合成的,因此对RC的材质有要求,R精度不小于1%,C的材质NPO或以上;同时对MCU也有要求,要求PWM1和PWM2更新的频率基本一致,更新误差不能超过1/2^DAC等效分辨率,可以通过示波器或者逻辑分析仪分析。
总结
分析单路的LPF参数以及PWM频率选择 分析多路PWM实现过程与要点